Задача
Четырёхугольник ABCD вписан в окружность, АС = а, BD = b, AB ⊥ CD. Найдите радиус окружности.
Решение
Пусть R – радиус окружности, ∠BAD = α, тогда ∠CDА = 90° – α (см. рис.). По следствию из теоремы синусов BD = 2R sin α, AC = 2R cos α. Следовательно, BD² + AC² = 4R², значит, R = 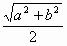 .
.
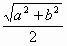
Ответ
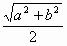 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет