Задача
В прямоугольном параллелепипеде АВСDA'B'C'D' АВ = ВС = а, AA' = b. Его ортогонально спроектировали на некоторую плоскость, содержащую ребро CD. Найдите наибольшее значение площади проекции.
Решение
Пусть плоскость проекции α расположена так, как показано на рисунке. Тогда проекция параллелепипеда совпадает с проекцией его диагонального сечения АВС'D'. Так как площадь ортогональной проекции многоугольника не превосходит площади многоугольника, то площадь проекции будет наибольшей, если α параллельна этому сечению. В этом случае Sпр = SABC'D' = AB·AD' = 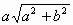 .
.
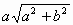
Ответ
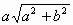 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет