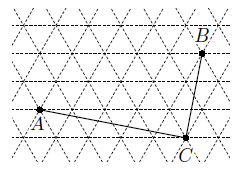
Решение 1:Продлив отрезок BC на его длину за точку C, получим точку D (рис. слева). Проведя отрезки AD и AB, заметим, что они равны, то есть треугольник ABD – равнобедренный. Так как AC – медиана этого треугольника, проведённая к его основанию, то AC – высота, то есть  ∠ACB = 90°.

               

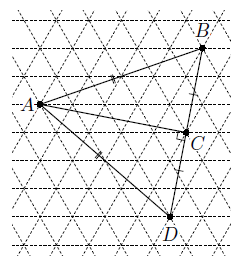
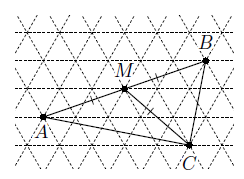
Решение 2:Рассмотрим треугольник ABC. Пусть M – середина AB (рис. справа). Заметим, что  AM = BM = CM,  то есть медиана треугольника равна половине стороны, к которой она проведена. Значит, треугольник ABC – прямоугольный:  ∠ACB = 90°.

90°.