Решение 1:Построим параллелограмм AKBP. Его диагонали делятся точкой пересечения пополам, то есть пересекаются в точке N и  PK = 2PN = PC.  Пусть прямые MB и CK пересекаются в точке T. Поскольку  MT || AK,  то MT – средняя линия треугольника AKC, откуда  KT = TC.  Значит, PT – медиана, проведённая к основанию равнобедренного треугольника KPC, откуда  PT ⊥ CK.  Следовательно, BT – медиана и высота треугольника BKC, значит,  AP = BK = BC.

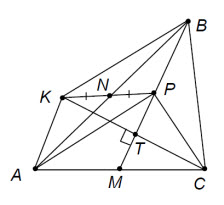
Решение 2:Обозначим через G точку пересечения медиан треугольника ABC. Тогда  CG : GN = 2 = CP : PN.  Значит, PG – биссектриса угла CPN. Следовательно,

∠BPN = ∠BPC.  Пусть X – середина PC. Тогда треугольники NPM и XPM равны по двум сторонам и углу между ними. Равные отрезки XM и NM являются средними линиями в треугольниках APC и ABC, значит,  AP = 2XM = 2NM = BC.

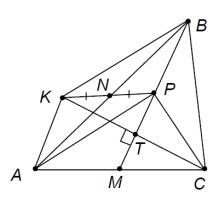
Решение 3:Рассмотрим такую точку Q, что P – середина AQ. Тогда MP – средняя линия треугольника CAQ, NP – средняя линия треугольника BAQ, значит, BQCP – равнобочная трапеция (BQ параллельна NP, поэтому не параллельна PC). Её диагонали BC и PQ равны, а  PQ = AP.

Ответ задачи отсутствует