Задача
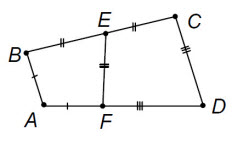
В выпуклом четырёхугольнике ABCD AD = АВ + CD. Оказалось, что биссектриса угла А проходит через середину стороны ВС.
Докажите, что биссектриса угла D также проходит через середину ВС.
Решение
Пусть E – середина BC. Отметим на стороне AD такую точку F, что AB = AF; тогда FD = CD. Треугольники AEB и AEF равны по двум сторонам и углу между ними. Значит, EF = BE = EC. Следовательно, треугольники DEF и DEC равны по трём сторонам, откуда ∠EDF = ∠EDC, и точка E лежит на биссектрисе угла D.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет