Задача
Через ортоцентр остроугольного треугольника проведены две перпендикулярные прямые. Стороны треугольника высекают на каждой из этих прямых два отрезка: один, лежащий внутри треугольника, второй – вне его. Докажите, что произведение двух внутренних отрезков равно произведению двух внешних.
Решение
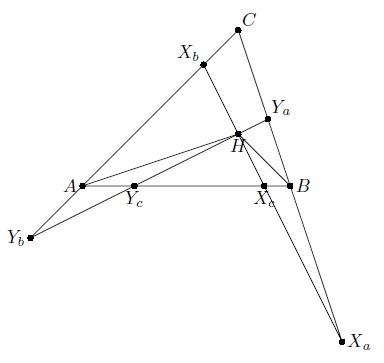
Пусть одна из прямых пересекает BC, CA, AB в точках Xa, Xb, Xc, а другая – в точках Ya, Yb, Yc (см. рис.). Тогда ∠HYaB = ∠XbHA и
∠HXbA = ∠YaHB, так как стороны этих углов перпендикулярны. Поэтому треугольники HBYa и XbAH подобны. Аналогично подобны треугольники HXaB и YbAH. Значит, AXb·BYa = AH·BH = AYb·BXa. С другой стороны, применив теорему Менелая к треугольникам CXaXb, CYaYb и прямой AB, получим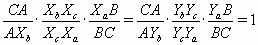 
. Из этих трёх равенств следует, что XbXc·YcYa = XcXa·YbYc.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь