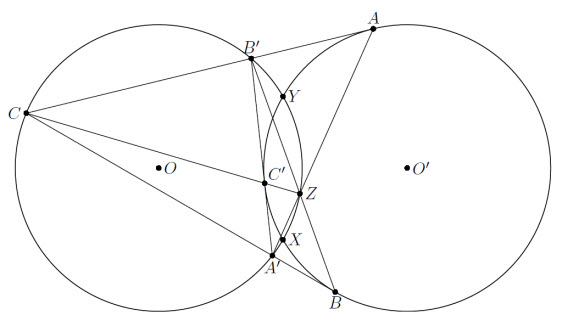
Пусть O, O' – центры окружностей. Легко видеть, что  OO' = .  По формуле Эйлера эти окружности для треугольника A'B'C являются описанной и вневписанной, то есть прямая A'B' касается второй окружности в точке C'. Согласно задаче 156915 точка C' лежит на прямой CZ (см. рис.).

  При этом  ∠AO'A'= ∠AO'C'+ ½ ∠C'O'B= 2∠ABC'+ ∠C'AB= ∠CB'A'+ ½ ∠CA'B'  (четырёхугольникиAB'C'O'иBA'C'O'– вписанные), ∠O'A'O= ∠O'A'B'+ ∠B'A'O=^π/₂– ∠C'O'A'+^π/₂– ∠CA'B'= π – ∠BCA– ½ ∠CA'B'= ∠CB'A'+ ½ ∠CA'B',  и, так как  O'A = OA',  тоAO'A'O– равнобедренная трапеция. Поэтому ∠O'AA'= ∠A'OO'.   Аналогично  ∠O'BB'= ∠B'OO'.  Следовательно,  ∠A'ZB'= 2π – ∠AO'B– ∠A'OB'= π – ∠C,  то есть точкаZлежит на описанной окружности треугольника и  ∠XZY= 150°.

150°.