Задача
Даны точки A, B. Найдите геометрическое место таких точек C, что C, середины отрезков AC, BC и точка пересечения медиан треугольника ABC лежат на одной окружности.
Решение
Пусть точка C принадлежит ГМТ и медианы AA0 и BB0 треугольника пересекаются в точке M. Тогда AM·AA0 = AB0·AC, то есть A0A² = ¾ AC². Аналогично B0B² = ¾ BC². Поскольку в любом треугольнике отношение суммы квадратов медиан к сумме квадратов сторон равно ¾ (см. задачу 155300), из этих равенств следует, что медиана из вершины C равна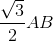 
. Нетрудно видеть, что любая точка окружности, кроме точек пересечения с прямой AB, входит в искомое ГМТ.
Ответ
Окружность с центром в середине AB и радиусом, равным 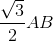без точек пересечения с прямой AB.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь