Задача
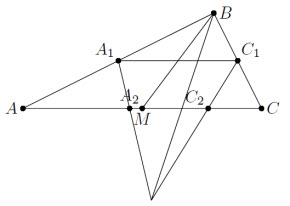
Пусть BM – медиана прямоугольного треугольника ABC (∠B = 90°). Окружность, вписанная в треугольник ABM, касается сторон AB, AM в точках A1, A2; аналогично определяются точки C1, C2. Докажите, что прямые A1A2 и C1C2 пересекаются на биссектрисе угла ABC.
Решение
Так как треугольники ABM, CBM – равнобедренные, точки A1, C1 – середины соответствующих катетов. Кроме того, прямая A1A2 перпендикулярна биссектрисе угла A и, значит, является биссектрисой угла AA1C1 (см. рис.). Аналогично C1C2 – биссектриса угла CC1A1. Следовательно, точка их пересечения – центр вневписанной окружности треугольника A1BC1 – лежит на биссектрисе угла B.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет