Назад
Задача 164908 • Сложность: 3 • 8-9 класс
Задача

На гипотенузе AC прямоугольного треугольника ABC отметили точку такую C1, что  BC = CC1.  Затем на катете AB отметили такую точку C2, что

AC2 = AC1;  аналогично определяется точка A2. Найдите угол AMC, где M – середина отрезка A2C2.

Авторы:
Швецов Д. В.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VIII Олимпиада по геометрии имени И.Ф. Шарыгина (2012 г.)
Количество версий:
4
Решение

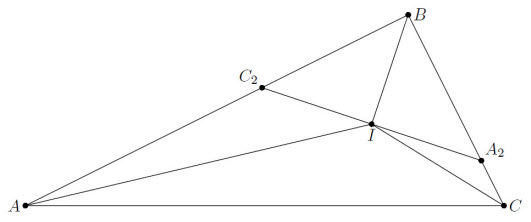
Пусть I – центр вписанной окружности треугольника ABC. Так как точка C1 симметрична B относительно CI, а C2 симметрична C1 относительно AI, то BI = IC2  и  ∠BIC2 = 90°.  Аналогично  BI = IA2  и  ∠BIA2 = 90°  (см.рис.). Следовательно, I совпадает с M, а  ∠AIC = 135°.

Ответ

135°.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет