Задача
Дан треугольник ABC. M – середина стороны BC, а P – проекция вершины B на серединный перпендикуляр к AC. Прямая PM пересекает сторону AB в точке Q. Докажите, что треугольник QPB равнобедренный.
Решение
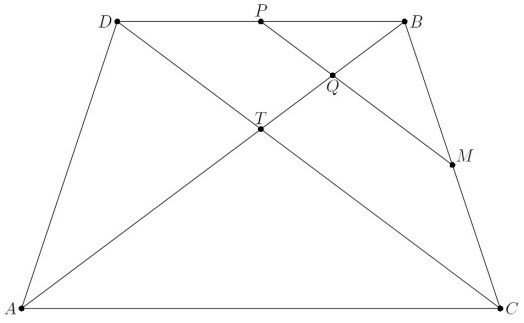
Пусть точка D симметрична B относительно серединного перпендикуляра к AC, а T – точка пересечения AB и CD. Тогда ACBD – равнобокая трапеция, и, значит, треугольник BDT – равнобедренный (см. рис.). Так как прямая PM содержит среднюю линию этого треугольника, треугольник QPB тоже равнобедренный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет