Задача
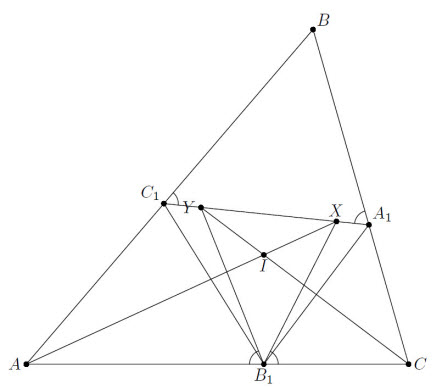
Окружность с центром I касается сторон AB, BC, CA треугольника ABC в точках C1, A1, B1. Прямые AI, CI, B1I пересекают A1C1 в точках X, Y, Z соответственно. Докажите, что ∠YB1Z = ∠XB1Z.
Решение
Так как B1I ⊥ AC, достаточно доказать, что ∠YB1A = ∠XB1C. Так как CI – серединный перпендикуляр к A1B1, то ∠YB1C = ∠YA1C. Значит,
∠YB1A = ∠C1A1B (см. рис.). Аналогично ∠XB1C = ∠A1C1B = ∠C1A1B.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет