Задача
В треугольнике ABC точка M – середина AB, а точка D – основание высоты CD. Докажите, что ∠A = 2∠B тогда и только тогда, когда AC = 2MD.
Решение
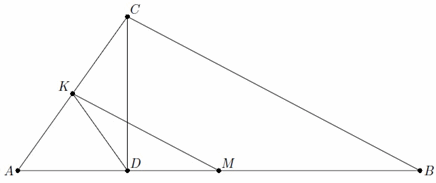
Пусть K – середина AC (см. рис.). Так как DK – медиана прямоугольного треугольника ADC, то AK = KD и ∠ADK = ∠A. С другой стороны, MK – средняя линия треугольника ABC, следовательно, ∠DMK = ∠B. Применяя к треугольнику DMK теорему о внешнем угле, получаем, что равенства
KD = DM и ∠KDA = 2∠KMD равносильны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет