Задача
Можно ли все натуральные делители числа 100! (включая 1 и само число) разбить на две группы так, чтобы в обеих группах было одинаковое количество чисел и произведение чисел первой группы равнялось произведению чисел второй группы?
Решение
100! делится на 31³, но не делится на 314. Поэтому все множители числа 100! можно разбить на четвёрки вида {n, 31n, 31²n, 31³n}, где n – произвольный делитель числа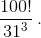 
Из каждой такой четвёрки числа n и 31³n поместим в одну группу, а числа 31n и 31²n – в другую.
Ответ
Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет