Задача
На доске был изображен пятиугольник, вписанный в окружность. Маша измерила его углы и у нее получилось, что они равны 80°, 90°, 100°, 130° и 140° (именно в таком порядке). Не ошиблась ли Маша?
Решение
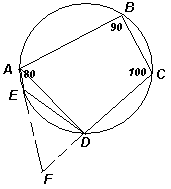
Пусть АВСDE – данный пятиугольник, в котором углы А, В, С, D и Е соответственно равны 80°, 90°, 100°, 130° и 140° (см. рис.). Далее можно рассуждать по-разному. Первый способ. Проведём диагональ AD, тогда четырёхугольник АВСD также вписанный, поэтому ∠BAD = 180° – ∠BСD = 80°. Таким образом,
∠BAD = ∠BAE, что невозможно.
Ответ
Ошиблась.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет