Задача
Правильный тетраэдр обладает таким свойством: для каждых двух его вершин найдётся третья вершина, образующая с этими двумя правильный треугольник. Существуют ли другие многогранники, обладающие этим свойством?
Решение
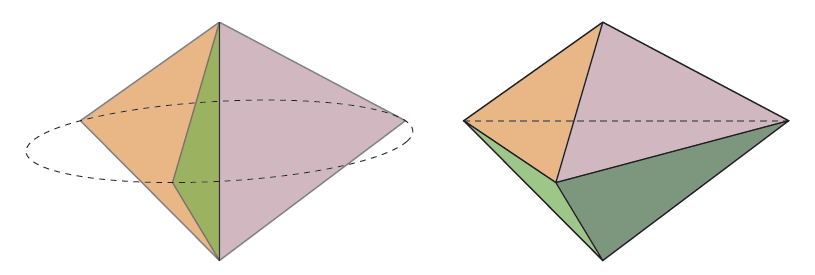
Зафиксируем две точки,AиB. Множеством точекX, для которых треугольникABXравносторонний, является окружность. Возьмём на этой окружности точкиC, D, Eтак, чтобы треугольникCDEбыл равносторонним. Многогранник с вершинамиA, B, C, D, Eобладает требуемым свойством. Действительно, каждая пара его вершин входит в один из равносторонних треугольниковABC, ABD, ABEиCDE. (Получившийся многогранник по-другому можно описать как две правильные треугольные пирамиды с высотой, равной половине боковой стороны, склеенные по основанию.)
Ответ
Существуют.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь