Число 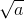    округляется в меньшую сторону до числа n, когда  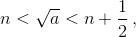   то есть когда  n² < a < n² + n + ¼.  Таким образом, корень из натурального числа a округляется "вниз", если a попадает на какой-то отрезок вида  [n² + 1, n² + n]  (на рисунке показаны такие отрезки для

n = 2, 3, 4, 5).

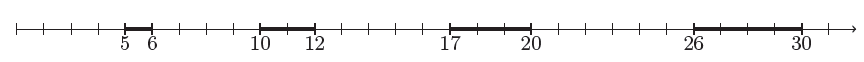
  Длина отрезка  [n² + 1,n² +n]  все время растет (она равна  n– 1)  и начиная с какого-тоnстановится больше разности нашей прогрессии. Значит, какой-то её член на этот отрезок точно попадёт ("делая шаги длиной 1 м лужу длиной 10 м не перешагнуть"). Соответствующее число будет округлено "вниз". Аналогично доказывается, что хотя бы одно число будет округлено вверх.

Не может.