Решение 1:   Из вписанности четырёхугольников BCPY и BAQX следует, что  ∠APY = ∠ABC = ∠CQX.  Пусть прямая, проходящая через M параллельно QX, пересекает прямую BC в точке K, а прямая, проходящая через M параллельно PY, пересекает прямую AB в точке L. Тогда  ∠AML = ∠ABC = ∠CMK,  откуда  ∠ALM = 180° – ∠LAM – ∠AML = 180° – ∠BAC –∠ABC = ∠ACB.  Значит, треугольники MAL и MKC подобны по двум углам.

  По условию  AP = AM – PM = PQ – PM = MQ;  аналогично  CQ = PM.  Отсюда  AY:YL = AP:PM = MQ:QC = KX:XC.  Значит,YиX– соответственные точки в подобных треугольникахMALиMKC. Следовательно,  ∠MXC= ∠MYL= ∠MYB.  Это и означает, что четырёхугольникBYMXвписан.

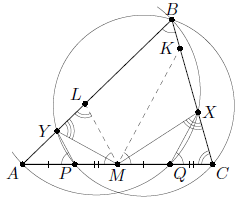
Решение 2:   Выберем на отрезке PQ такую точку Z, что  CQ = QZ.  Тогда  AP + QC = AC – PQ = PQ,  PZ = PQ – QZ = PQ – QC = AP.

  Из вписанности четырёхугольникаBYPCимеем  AB·AY = AP·AC= 2AP·^AC/₂=AZ·AM.  АналогичноCX·CB = CZ·CM.   Если  Z ≠ M,  полученные равенства означают, что каждая из четвёрок точекB, Y, Z, MиB, X, Z, Mлежит на одной окружности, то есть точкиXиYлежат на описанной окружности треугольникаBMZ.   Если же  Z = M,  то те же равенства означают, что точкиXиYлежат на (единственной!) окружности, проходящей черезBи касающейсяACв точкеM.

Ответ задачи отсутствует