Задача
В республике математиков выбрали число α > 2 и выпустили монеты достоинствами в 1 рубль, а также в αk рублей при каждом натуральном k. При этом α было выбрано так, что достоинства всех монет, кроме самой мелкой, иррациональны. Могло ли оказаться, что любую сумму в натуральное число рублей можно набрать этими монетами, используя монеты каждого достоинства не более 6 раз?
Решение
Покажем, что математики могли выбрать число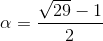 
– корень уравнения α² + α = 7. Ясно, что α > 2. Нетрудно видеть, что при натуральных m 
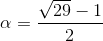где am и bm – целые числа, причём am < 0 < bm при нечётных m и am > 0 > bm при чётных m. Значит, число αm иррационально.
Осталось показать, что для любого натурального числа n сумму в n рублей можно набрать требуемым способом. Рассмотрим все способы набрать n рублей выпущенными монетами (хотя бы один такой способ существует: можно взять n рублёвых монет). Выберем из них способ, в котором наименьшее число монет. Предположим, что какая-то монета достоинства αk (k ≥ 0) встречается в этом способе хотя бы 7 раз. Тогда можно заменить 7 монет по αk монетами достоинств αk+1 и αk+2. При этом суммарное достоинство монет не изменится (αk+1 + αk+2 = 7αk), а их количество уменьшится. Это противоречит выбору нашего способа.
Ответ
Могло.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь