Задача
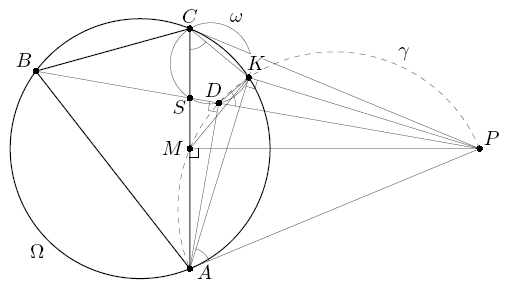
Точка M – середина стороны AC остроугольного треугольника ABC, в котором AB > BC. Касательные к описанной окружности Ω треугольника ABC, проведённые в точках A и C, пересекаются в точке P. Отрезки BP и AC пересекаются в точке S. Пусть AD – высота треугольника BP. Описанная окружность ω треугольника CSD второй раз пересекает окружность Ω в точке K. Докажите, что ∠CKM = 90°.
Решение
Точки M и D лежат на окружности γ с диаметром AP. Так как точки C, K, D и S лежат на окружности ω, ∠KDP = ∠ACK = ∠KAP, то есть точки A, D, K и P лежат на одной окружности. Следовательно, ∠AKP = ∠ADP = 90° (см.рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет