Задача
Можно ли правильную треугольную призму разрезать на две равные пирамиды?
Решение
Пусть M – середина бокового ребра AA' призмы ABCA'B'C. Тогда пирамиды A'B'BMC' и C'CAMB равны (см. рис.). Это можно доказать различными способами.
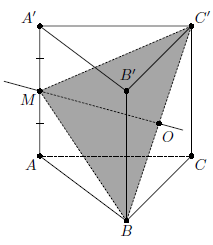
Ответ
Можно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет