Задача
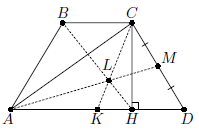
В трапеции ABCD BC < AD, AB = CD, K – середина AD, M – середина CD, CH – высота.
Докажите, что прямые AM, CK и BH пересекаются в одной точке.
Решение
AM и CK – медианы треугольника ACD, следовательно, точка L их пересечения делит отрезок CK в отношении 2 : 1 (см. рис.). Кроме того,
BC : KH = 2 : 1, поскольку KH = ½ AD – ½ (AD – BC) = ½ BC. Из параллельности AD и BC теперь следует, что BH делит отрезок CK в отношении 2 : 1, то есть проходит через точку L.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет