Пусть X – точка пересечения описанных окружностей треугольников PBC и QBA, а  ∠QBC = ∠BCQ = α  (см. рис.). Тогда  ∠AQB = 2α. Из равенства вписанных углов, опирающихся на одну дугу, получим, что  ∠PXB = ∠PCB = α  и  ∠AXB = ∠AQB = 2α.  Следовательно, XP – биссектриса угла X в треугольнике AXB.

  Докажем, что точки X, P и K лежат на одной прямой.

  Первый способ. Серединный перпендикуляр KP к стороне AB и биссектриса XP угла X кроме общей точки P имеют ещё одну общую точку: середину дуги AB описанной окружности треугольника AXB. Следовательно, эти прямые совпадают.   Второй способ. Рассмотрим отдельно треугольник AXB (см. рис.). В треугольниках AXP и BXP равны две стороны и угол, противолежащий одной из этих сторон. Следовательно, либо эти треугольники равны, либо  ∠PAX + ∠PBX = 180°.  Второй случай невозможен, поскольку тогда сумма углов треугольника AXB будет больше 180°. Следовательно,  AX = XB,  то есть X лежит на серединном перпендикуляре к стороне AB.   Аналогично можно доказать, что точки X, Q и L лежат на одной прямой.

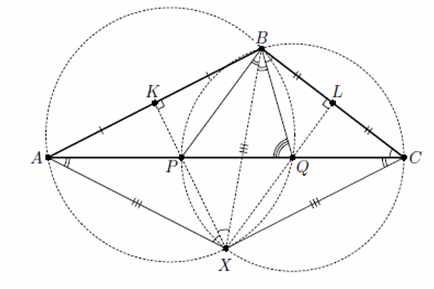
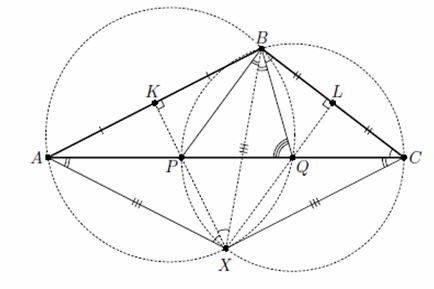
  Из доказанного следует, что  AX = XB = XC,  то есть  ∠PBX = ∠XCA = ∠XAC = ∠QBX,  поэтому BX – биссектриса угла PBQ.

Ответ задачи отсутствует