Задача
Существует ли выпуклый пятиугольник, в котором каждая диагональ равна какой-то стороне?
Решение
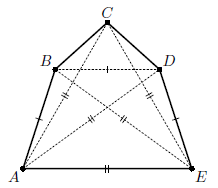
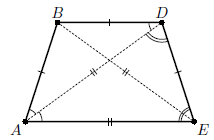
На рисунке изображен пятиугольник ABCDE, у которого диагонали AC, AD, BE и CE равны стороне AE, а диагональ BD равна сторонам AB и DE. Покажем, как он может быть получен.
Ответ
Существует.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет