Назад
Задача 164695 • Сложность: 2 • 6-7 класс
Задача

Два угла прямоугольного листа бумаги согнули так, как показано на рисунке. Противоположная сторона при этом оказалась разделённой на три равные части. Докажите, что закрашенный треугольник – равносторонний.

Авторы:
Шаповалов А. В.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Московская устная олимпиада для 6-7 классов 12 (2014 год) 7 класс
Количество версий:
3
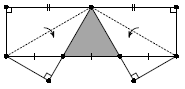
Решение

Введём обозначения так, как показано на рисунке.

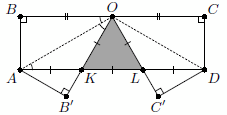
Треугольник AB'O получился перегибанием из треугольника ABO, значит, эти треугольники равны. Следовательно,  ∠AOB = ∠AOB'.  Кроме того, из параллельности сторон AD и BC прямоугольника следует, что  ∠AOB = ∠KAO.  Таким образом, в треугольнике AOK углы AOK и KAO равны, значит, этот треугольник равнобедренный:  OK = AK. Рассуждая аналогично, получим, что треугольник DOL – также равнобедренный. Следовательно,

OK = OL = KL,  то есть треугольник KOL – равносторонний.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет