Задача
На клетчатой доске размером 4×4 Петя закрашивает несколько клеток. Вася выиграет, если сможет накрыть все эти клетки не пересекающимися и не вылезающими за границу квадрата уголками из трёх клеток. Какое наименьшее количество клеток должен закрасить Петя, чтобы Вася не выиграл?
Решение
Так как 16 не делится на 3, то всю доску (16 клеток) нельзя покрыть не пересекающимися и не вылезающими за границу квадрата уголками из трёх клеток.
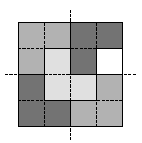
Покажем, что любые 15 покрашенных клеток можно покрыть такими уголками. Разобьём квадрат 4×4 на четыре квадрата размером 2×2, тогда единственная не покрашенная клетка попала в какой-то один из них. Любые три полностью покрашенных квадрата можно покрыть уголками из трёх клеток (см. рис.), а в четвёртом квадрате любые три покрашенные клетки всегда можно покрыть одним уголком.
Ответ
16 клеток.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь