Задача
Плоскость α пересекает рёбра AB, BC, CD и DA треугольной пирамиды ABCD в точках K, L, M и N соответственно. Оказалось, что двугранные углы
∠(KLA, KLM), ∠(LMB, LMN), ∠(MNC, MNK) и ∠(NKD, NKL) равны. (Через ∠(PQR, PQS) обозначается двугранный угол при ребре PQ в тетраэдре PQRS.) Докажите, что проекции вершин A, B, C и D на плоскость α лежат на одной окружности.
Решение
Обозначим через A', B', C', D' проекции вершин A, B, C, D на плоскость α. Пусть X – произвольная точка на продолжении отрезка KL за точку K. Тогда
∠(KXA,KXN) = ∠(KLA, KLM) и ∠(KNA, KNX) = ∠(NKD, NKL). По условию эти углы равны; значит, в трёхгранном угле KANX (с вершиной K) двугранные углы при ребрах KN и KX равны между собой. Это означает, что плоскость, проходящая через прямую KA и перпендикулярная плоскости α, – это плоскость симметрии трёхгранного угла KANX. Поэтому точка A' лежит на прямой, содержащей биссектрису угла XKN, то есть на внешней биссектрисе угла NKL.
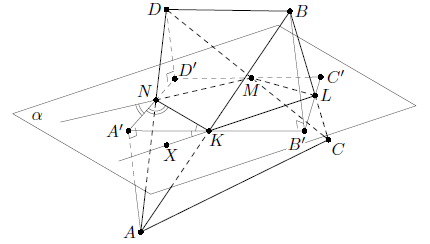
Из треугольника A'KN находим ∠B'A'D' = ∠KA'N = 180° – ∠A'KN – ∠A'NK = (90° – ∠A'KN) + (90° – ∠A'NK) = ½ (∠NKL + ∠MNK). Аналогично получаем, что ∠B'C'D' = ½ (∠KLM + ∠LMN). Таким образом, ∠B'A'D' + ∠B'C'D' = ½ (∠NKL + ∠MNK + ∠KLM + ∠LMN) = 180°, откуда и следует, что четырёхугольник A'B'C'D' – вписанный.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь