Задача
На доске написано выражение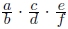 
, где a, b, c, d, e, f – натуральные числа. Если число a увеличить на 1, то значение этого выражения увеличится на 3. Если в исходном выражении увеличить число c на 1, то его значение увеличится на 4; если же в исходном выражении увеличить число e на 1, то его значение увеличится на 5. Какое наименьшее значение может иметь произведение bdf?
Решение
Произведение знаменателей может быть равным 60. Один из возможных примеров: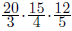 
. Оценка. Пусть значение исходного выражения равно A. Тогда в результате первой операции произведение примет значение 
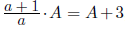, откуда
A = 3a. Значит, A – натуральное число, кратное 3. Аналогично доказывается, что A = 4c = 5e. Далее можно рассуждать по-разному. Первый способ. Ясно, что A делится на 3·4·5 = 60, поэтому A ≥ 60.
Переписав равенство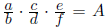 
в виде 
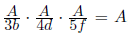, получаем 60bdf = A² ≥ 60², откуда bdf ≥ 60. Второй способ. Имеем 
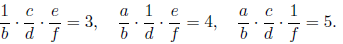Умножив первое равенство на второе и разделив на третье, получаем, что 
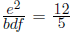. Поскольку дробь справа несократима, знаменатель bdf делится на 5. Аналогично доказывается, что он делится на 3 и на 4, откуда следует, что он делится на 60, то есть не меньше 60.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь