Задача
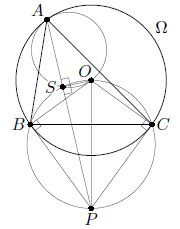
Треугольник ABC вписан в окружность Ω с центром O. Окружность Ω1, построенная на AO как на диаметре, пересекает описанную окружность Ω2 треугольника OBC в точке S, отличной от O. Касательные к Ω в точках B и C пересекаются в точке P. Докажите, что точки A, S и P лежат на одной прямой.
Решение
Поскольку CP и BP – касательные к Ω, ∠OBP = ∠OCP = 90°; значит, точка P лежит на Ω2 и PO – диаметр этой окружности (см. рис.). Поэтому
∠OSP = 90°. Поскольку AO – диаметр окружности Ω1, ∠ASO = 90°. Таким образом, точки A и P лежат на перпендикуляре к OS, проходящем через точку S.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет