Задача
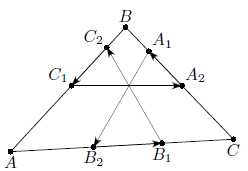
На стороне AB треугольника ABC выбраны точки C1 и C2. Аналогично на стороне BC выбраны точки A1 и A2, а на стороне AC – точки B1 и B2. Оказалось, что отрезки A1B2, B1C2 и C1A2 имеют равные длины, пересекаются в одной точке, и угол между каждыми двумя из них равен 60°. Докажите, что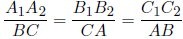 
.
Решение
Заметим, что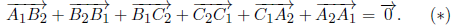 
По условию A1B2 = B1C2 = C1A2, и угол между каждыми двумя из трёх прямых A1B2, B1C2, C1A2 равен 60°. Поэтому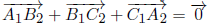 
. Отсюда и из (*) получаем
.
, 
, 
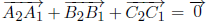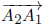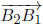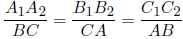от некоторой точки последовательно друг за другом, мы получим некоторый треугольник T. Стороны треугольника T параллельны соответствующим сторонам треугольника ABC, поэтому эти треугольники подобны. Отсюда и вытекает требуемое равенство.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет