Задача
Стозначное натуральное число n назовём необычным, если десятичная запись числа n³ заканчивается на n, а десятичная запись числа n² не заканчивается на n. Докажите, что существует не менее двух стозначных необычных чисел.
Решение
Например, такими числами являются n1 = 10100 – 1 = 99...9 и n2 = 5·1099 – 1. Действительно, числа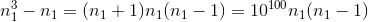 
и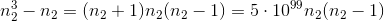 
делятся на 10100; это означает, что
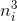оканчивается на ni. С другой стороны, числа 
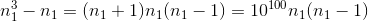не делятся на 5 (и тем более на 10100); значит, 
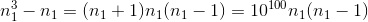не оканчивается на ni.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет