Задача
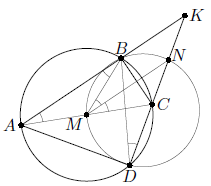
Дан вписанный четырёхугольник ABCD. Лучи AB и DC пересекаются в точке K. Оказалось, что точки B, D, а также середины M и N отрезков AC и KC лежат на одной окружности. Какие значения может принимать угол ADC?
Решение
MN – средняя линия в треугольнике AKC, поэтому ∠BAC = ∠NMC. Кроме того, ∠BAC = ∠BDC, так как четырёхугольник ABCD – вписанный.
Пусть точки M и N лежат с одной стороны от прямой BD. Тогда M лежит внутри треугольника BCD и, тем более, внутри треугольника BND, а значит, и внутри его описанной окружности. Но тогда точки B, N, D и M не могут лежать на одной окружности. Значит, N и M лежат по разные стороны от BD, и ∠BDC = ∠BMN.
Из параллельности MN и AK вытекает, что ∠BMN = ∠ABM, откуда ∠BAC = ∠BDC = ∠ABM. Отсюда получаем AM = MB, то есть в треугольнике ABC медиана BM равна половине стороны AC. Следовательно, ∠ABC = 90°, а значит, и ∠ADC = 90°.
Ответ
90°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь