Решение 1:   Пусть O – точка пересечения диагоналей AC и BD (см. рис). Биссектрисы углов ADB и DAC пересекаются в центре O₁ вписанной окружности треугольника AOD, а биссектрисы углов ACB и DBC – в центре O₂ вписанной окружности треугольника BOC. Значит, точки O₁ и O₂ лежат на общей биссектрисе вертикальных углов AOD и BOC.

  Рассмотрим ромб PO₁QO₂ из условия задачи. В нём  ∠PO₁O₂ = ∠QO₁O₂,  а значит,  ∠DO₁O = ∠AO₁O.  Следовательно, треугольники AOO₁ и DOO₁ равны по стороне (O₁O – общая) и двум прилежащим углам, откуда  AO = DO.  Отсюда  ∠OAD = ∠ODA,  и четырёхугольник ABCD симметричен относительно серединного перпендикуляра к AD. Поэтому  AB = CD.

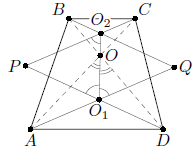
Решение 2:   Обозначим вершины ромба через P, O₁, Q, O₂, как и в решении 1. Расстояние между прямыми O₂P и O₁Q равно расстоянию между прямыми O₁P и O₂Q, то есть  AC sin(½∠CAD) = BD sin(½∠BDA).

  Так как вершины B и C равноудалены от прямой AD, имеем  AC sin ∠CAD = BD sin∠BDA.

  Деля второе полученное равенство на первое, получаем  cos(½∠CAD) = cos(½∠BDA).

  Так как оба угла CAD и BDA меньше 180°, получаем, что  ∠CAD = ∠BDA.  Как и в решении 1, заключаем, что  AB = CD.

Ответ задачи отсутствует