Пусть K, L, M, N – точки на сторонах AB, BC, CD, DA пространственного четырёхугольника ABCD, являющиеся основаниями общих перпендикуляров. При проекции на плоскость, параллельную KM и LN, эти прямые перейдут в перпендикулярные прямые K'M' и L'N'. По теореме о трёх перпендикулярах проекции прямых AB и CD будут перпендикулярны K'M', а проекции прямых BC и AD перпендикулярны L'N'. Следовательно, четырёхугольник ABCD проецируется в прямоугольник A'B'C'D', причём  A'K' = D'M',  B'L' = A'N'.  Значит,  AK : KB = DM : MC,  BL : LC = AN : ND.  Пусть P и Q – соответственно точки пересечения KL и MN с AC. По теореме Менелая 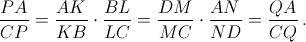    Поэтому точки P и Q совпадают, откуда и следует, что точки K, L, M, N лежат в одной плоскости.

Ответ задачи отсутствует