Задача
Дана окружность ω и точка A вне её. Через A проведены две прямые, одна из которых пересекает ω в точках B и C, а другая – в точках D и E (D лежит между A и E). Прямая, проходящая через D и параллельная BC, вторично пересекает ω в точке F, а прямая AF – в точке T. Пусть M – точка пересечения прямых ET и BC, а N – точка, симметричная A относительно M. Докажите, что описанная окружность треугольника DEN проходит через середину отрезка BC.
Решение
Спроецируем сначала прямую AB на окружность из точки D, а затем окружность на прямую AB из точки T. В результате A перейдёт в M, бесконечно удалённая точка – в A, а точки B и C останутся на месте. Приравняв двойные отношения, получим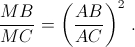 
Из этого соотношения и равенства MC – MB = AC – AB находим 
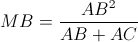и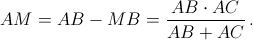 
Пусть K – середина BC. Тогда
AN·AK = 2AM·½ (AB + AC) = AB·AC = AD·AE, то есть точки D, E, K, N лежат на одной окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь