Задача
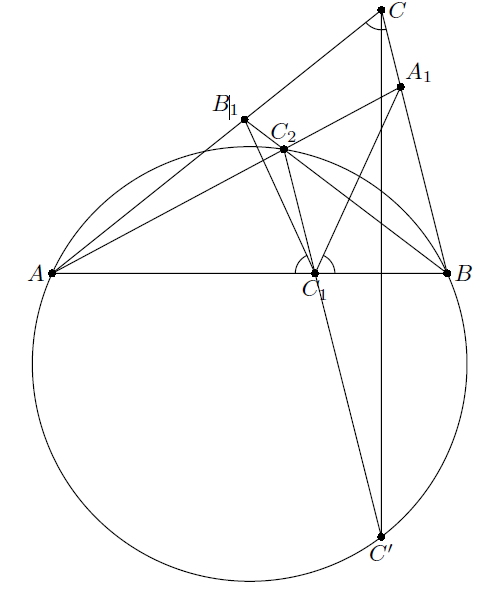
На стороне AB треугольника ABC взята произвольная точка C1. Точки A1, B1 на лучах BC и AC таковы, что ∠AC1B1 = ∠BC1A1 = ∠ACB. Прямые AA1 и BB1 пересекаются в точке C2. Докажите, что все прямые C1C2 проходят через одну точку.
Решение
Из условия следует, что четырёхугольники ACA1C1 и BCB1C1 – вписанные. Поэтому ∠B1BC1 = ∠ACC1, ∠A1AC1 = ∠BCC1, а значит,
∠AC2B = π – ∠C, то есть C2 лежит на окружности, проходящей через A, B и точку C’, симметричную C относительно AB. При этом
∠BC'C1 = ∠BCC1 = ∠AC1C – ∠ABC = ∠AA1C – ∠ABC = ∠BAC2, следовательно, прямая C'C1 проходит через C2 (см. рис.). Таким образом, все прямые C1C2 проходят через точку C'.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет