Назад
Задача 164472 • Сложность: 3 • 9-11 класс
Задача

Дан вписанный четырёхугольник, острый угол между диагоналями которого равен φ. Докажите, что острый угол между диагоналями любого другого четырёхугольника с теми же длинами сторон (идущими в том же порядке) меньше φ.

Авторы:
Заславский А. А.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина IX Олимпиада по геометрии имени И.Ф. Шарыгина (2013 г.) Заочный тур
Количество версий:
3
Решение

Пусть диагонали четырёхугольника ABCD пересекаются в точке P, , а угол между ними равен ψ. Обозначим  PA = a,  PB = b,  PC = c,  PD = d.  По теореме косинусов   |AB² – BC² + CD² – CA²| = 2cos ψ (ab + bc + cd + da) = 2AC·BD cos ψ.   Но по неравенству Птолемея (см. задачу 158396 а)

AC·BD ≤ AB·CD + BC·AD,  причём равенство достигается только на вписанном четырёхугольнике. Поэтому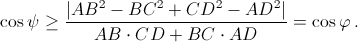

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет