Задача
Вписанная в треугольник ABC окружность касается сторон BC, CA, AB в точках A', B', C' соответственно. Перпендикуляр, опущенный из центра I этой окружности на медиану CM, пересекает прямую A'B' в точке K. Докажите, что CK || AB.
Решение
При полярном преобразовании относительно вписанной окружности указанный перпендикуляр перейдёт в бесконечно удалённую точку медианы CM, прямая A'B' – в точку C, а прямая, проходящая через C и параллельная AB, – в точку P пересечения A'B' с IC'. Таким образом, надо доказать, что эта точка лежит на медиане.
Поскольку IA' = IB', ∠PIB' = ∠A, ∠PIA' = ∠B, то по теореме синусов B'P : A'P = BC : AC. А так как CA' = CB', то sin∠ACP : sin∠BCP = BC : AC, то есть CP делит AB пополам (см. рис.).
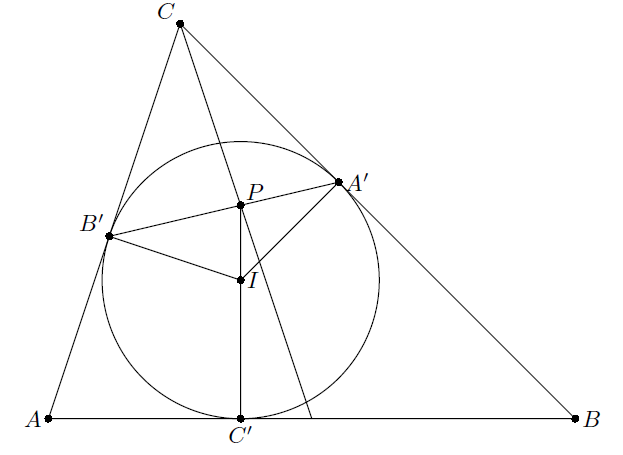
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь