Задача
а) В треугольник ABC вписаны треугольники A1B1C1 и A2B2C2 так, что C1A1 ⊥ BC, A1B1 ⊥ CA, B1C1 ⊥ AB, B2A2 ⊥ BC, C2B2 ⊥ CA,
A2C2 ⊥ AB. Докажите, что эти треугольники равны.б) Внутри треугольника ABC взяли точки A1, B1, C1, A2, B2, C2 так, что A1 - на отрезке AB1, B1 - на отрезке BC1, C1 – на отрезке CA1, A2 – на отрезке AC2, B2 – на отрезке BA2, C2 – на отрезке CB2 и углы BAA1, CBB1, ACC1, CAA2, ABB2, BCC2 равны. Докажите, что треугольники A1B1C1 и A2B2C2 равны.
Решение
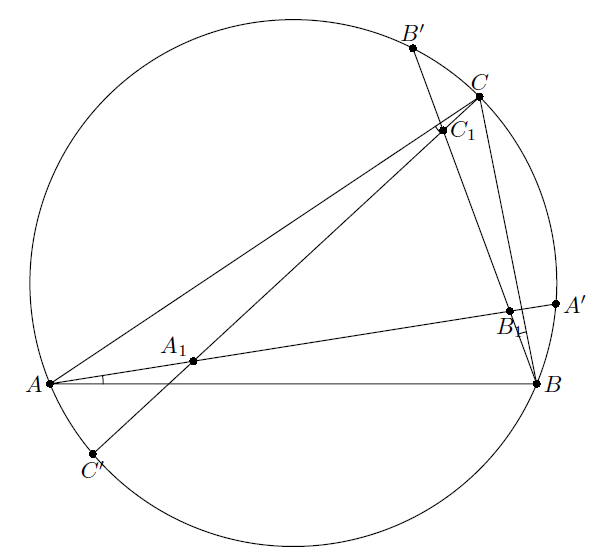
а) Опишем вокруг треугольника A2B2C2 треугольник A'B'C' так, что C2A2 ⊥ B'C', A2B2 ⊥ C'A', B2C2 ⊥ A'B'. Очевидно, что соответствующие стороны треугольников ABC и B'C'A' симметричны относительно центра описанной окружности треугольника A2B2C2. При этой симметрии треугольник A2B2C2 переходит в треугольник B1C1A1. Следовательно, эти треугольники равны и имеют общий центр описанной окружности. б) B описанной окружности треугольника ABC рассмотрим хорды AA', BB', CC', AA'', BB'', CC'', лежащие соответственно на прямых A1B1, B1C1, C1A1, A2C2, B2A2, C2B2 (см. рис.). Из условия следует равенство дуг AC', BA', CB', AB'', CA'', BC''. Тогда при повороте вокруг центра описанной окружности хорды AA', BB', CC' переходят соответственно в BB'', CC'', AA'', значит, этот поворот совмещает треугольники A1B1C1 и B2C2A2.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь