Задача
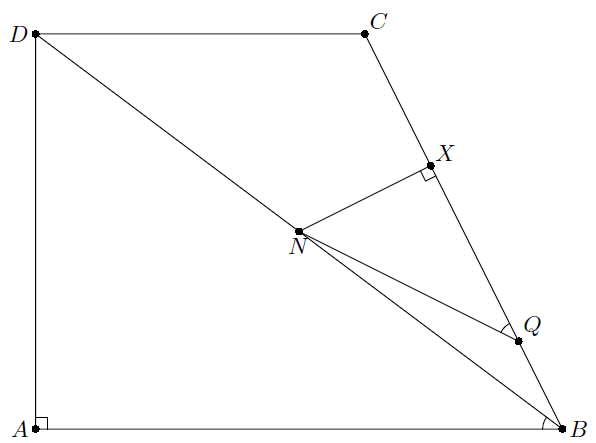
Точки M, N – середины диагоналей AC, BD прямоугольной трапеции ABCD (∠A = ∠D = 90°). Описанные окружности треугольников ABN, CDM пересекают прямую BC в точках Q, R. Докажите, что точки Q, R равноудалены от середины отрезка MN.
Решение
Пусть X, Y – проекции точек N и M на BC. Тогда утверждение задачи равносильно равенству RY = XQ. Заметим, что треугольник ANB – равнобедренный (AN – медиана прямоугольного треугольника BAD). Так как ∠NQX = ∠NAB = ∠DBA (см. рис.), то
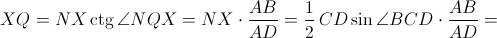
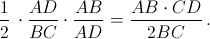
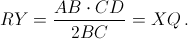
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет