Назад
Задача 164468 • Сложность: 3 • 9-10 класс
Задача

Пусть A1 и C1 – точки касания вписанной окружности со сторонами BC и AB соответственно, а A' и C' – точки касания вневписанной окружности треугольника, вписанной в угол B, с продолжениями сторон BC и AB соответственно. Докажите, что ортоцентр H треугольника ABC лежит на A1C1 тогда и только тогда, когда прямые A'C1 и BA перпендикулярны.

Авторы:
Ивлев Ф.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина IX Олимпиада по геометрии имени И.Ф. Шарыгина (2013 г.) Заочный тур
Количество версий:
4
Решение

  Пусть  A'C1 ⊥ BA.  Тогда и  C'A1 ⊥ BC  (так как A1С1C'A' – равнобедренная трапеция). По теореме Фалеса высота, опущенная из точки C на AB, делит отрезок A1C1 в отношении 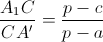    (см. задачу 155404). Так же доказывается, что высота, опущенная из точки A на BC, проходит через ту же точку.   Обратное утверждение доказывается аналогично.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет