Задача
Пусть T1, T2 – точки касания вневписанных окружностей треугольника ABC со сторонами BC и AC соответственно. Оказалось, что точка, симметричная центру вписанной окружности треугольника относительно середины AB, лежит на описанной окружности треугольника CT1T2. Найдите угол BCA.
Решение
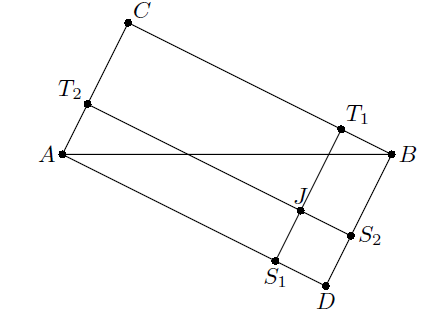
Пусть D – четвёртая вершина параллелограмма ACBD, J – центр вписанной окружности треугольника ABD, S1, S2 – точки касания этой окружности с AD и BD. Тогда DS1 = BT1 (см. задачу 155404), поэтому S1T1 || AC. Аналогично S2T2 || BC, то есть CT1JT2 – параллелограмм. Но по условию он вписан, следовательно, является прямоугольником.
Ответ
90°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет