Назад
Задача 164462 • Сложность: 3 • 8-10 класс
Задача

Пусть BD – биссектриса треугольника ABC. Точки Ia, Ic – центры вписанных окружностей треугольников ABD, CBD. Прямая IaIc пересекает прямую AC в точке Q. Докажите, что  ∠DBQ = 90°.

Авторы:
Швецов Д. В.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина IX Олимпиада по геометрии имени И.Ф. Шарыгина (2013 г.) Заочный тур
Количество версий:
3
Решение

Прямые AIa и CIc пересекаются в центре I вписанной окружности треугольника ABC. При этом  AIa : IaI = AD : ID, CIc : IcI = CD : ID.  По теореме Менелая 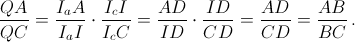    Следовательно, BQ – внешняя биссектриса угла B, что и требовалось.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет