Задача
Дан неравнобедренный треугольник ABC. Точка O – центр его описанной окружности, а точка K – центр описанной окружности ω треугольника BCO. Высота треугольника ABC, проведенная из точки A, пересекает окружность ω в точке P. Прямая PK пересекает описанную окружность треугольника ABC в точках E и F. Докажите, что один из отрезков EP и FP равен отрезку PA.
Решение
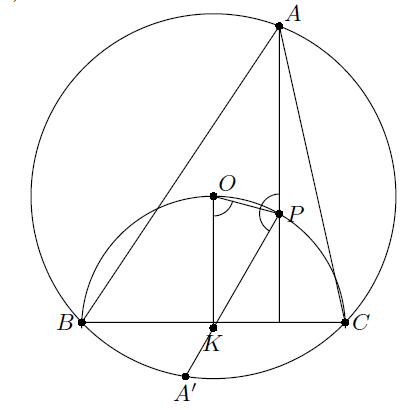
Так как точки O, K лежат на серединном перпендикуляре к BC, то OK || AP. Поэтому ∠OPK = ∠POK = ∠OPA. Значит, точка A', симметричная A относительно OP, лежит на прямой PK. При этом OA' = OA, то есть A' лежит на описанной окружности треугольника ABC (см. рис.) и, следовательно, совпадает с одной из точек E, F.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь