Задача
В равнобедренном треугольнике ABC (AC = BC) угол при вершине C равен 20°. Биссектрисы углов A и B пересекают боковые стороны треугольника соответственно в точках A1 и B1. Докажите, что треугольник A1OB1 (где O – центр описанной окружности треугольника ABC) является равносторонним.
Решение
Решение 1:Возьмём на сторонах BC и AC точки A' и B' так, что AB' = B'O = OA' = A'B. Очевидно, A'B' || AB, то есть ∠CA'B' = ∠CAB = 80°. Кроме того,
∠A'OB = ∠A'BO = ∠BCO = 10°. Значит, ∠CA'O = 20°, а ∠OA'B' = 60°, то есть треугольник OA'B' – равносторонний. Тогда A'B' = A'B и
∠A'BB' = ∠A'B'B = ∠ABB' (рис. слева). Следовательно, точка B' совпадает с B1. Аналогично A' совпадает с A1, что и требовалось.
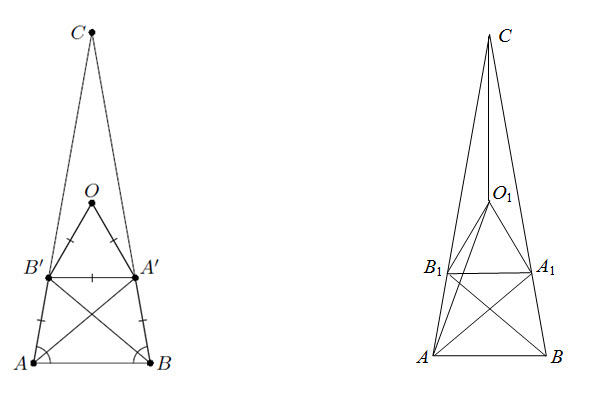
Решение 2:Очевидно, A1B1 || AB, поэтому ∠B1A1A = ∠BAA1 = ∠B1AA1 = 40╟. Значит, B1A = B1A1. Построим равносторонний треугольник A1O1B1 (O1 находится с той же стороны от прямой A1B1, что и точка C, рис. справа). В силу симметрии точка O1 лежит на биссектрисе угла C. Кроме того, B1A = B1A1 = B1O1. Угол при вершине равнобедренного треугольника AB1O1 равен 160°, значит, угол B1AO1 при его основании равен 10°. Следовательно, в треугольнике AO1C ∠CAO1 = ∠O1CA, то есть O1A = O1C. Аналогично O1B = O1C, значит, O1 совпадает с O.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь