Задача
На рисунке изображена снежинка, симметричная относительно поворота вокруг точки O на 60° (при этом повороте каждый луч снежинки переходит в другой луч) и отражения относительно прямой OX. Найдите отношение длин отрезков OX : XY. (Пунктирными линиями показаны точки, лежащие на одной прямой.)
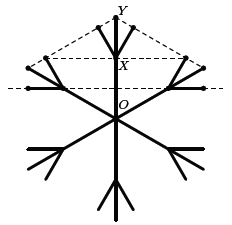
Решение
Вместо отношения OX : XY будем искать равное ему отношение OX' : X'Y' (см. рис.).
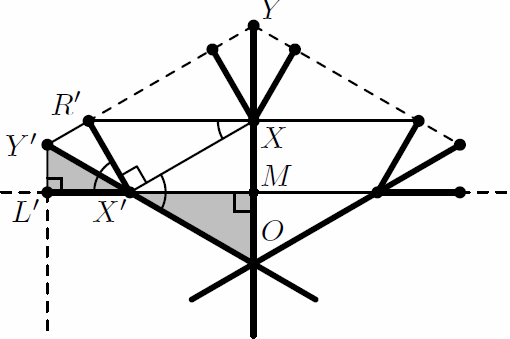
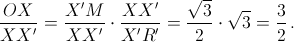 Второй способ. Пусть C – точка пересечения прямых Y'Y'' и LR'''.
Второй способ. Пусть C – точка пересечения прямых Y'Y'' и LR'''. 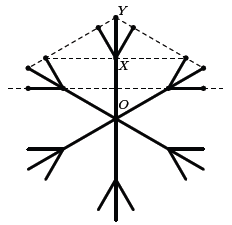
Ответ
3 : 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет