Задача
В пространстве отмечены пять точек. Известно, что это центры сфер, четыре из которых попарно касаются извне и касаются изнутри пятой сферы. При этом невозможно определить, какая точка является центром объемлющей сферы. Найдите отношение радиусов наибольшей и наименьшей сферы.
Решение
Пусть O и O' – два возможных положения центра большой сферы (среди данных пяти точек), а A, B, C – три оставшиеся отмеченные точки.
Рассмотрим точки O, O', A, B. Пусть в конфигурации, когда O – центр большой сферы, радиусы сфер с соответствующими центрами равны R, r', ra и rb. Тогда OO' = R' – r', OA = R – ra, OB = R – rb, O'A = r' + ra, O'B = r' + rb, AB = ra + rb, откуда OO' – AB = OA – O'B = OB – O'A; обозначим эту разность через d. Аналогично из конфигурации, в которой O' – центр большой сферы, имеем d = OO' – AB = O'A – OB = O'B – OA = – d. Значит, d = 0, то есть OO' = AB, OA = O'B, OB = O'A.
Рассматривая аналогично четвёрки точек (O, O', A, C) и (O, O', B, C), получаем OO' = AB = AC = BC и OA = O'B = OC = O'A = OB = O'C. Итак, треугольник ABC – правильный (пусть его сторона равна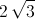 
), а правильные пирамиды OABC и O'ABC равны; значит, O и O' симметричны относительно плоскости (ABC). Кроме того, 
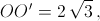то есть высота каждой пирамиды равна 
. Пусть H – общее основание этих высот, тогда и HA = HB = HC = 2, откуда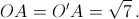 
Значит, радиусы трёх сфер с центрами в A, B, C равны , а радиусы остальных двух сфер равны 
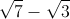и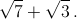 
Ответ
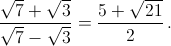
Чтобы оставлять комментарии, войдите или зарегистрируйтесь