Решение 1:   Пусть N – проекция точки C на A₁B₁ (см. рис.). Рассмотрим гомотетию с центром в точке C, при которой H перейдет в C₁, P – в P₁, Q – в Q₁. Тогда C₁P₁ ⊥ C₁B₁,  C₁Q₁ ⊥ C₁A₁,  и достаточно доказать, что прямая CN проходит через середину P₁Q₁.

  Пусть K и L – проекции точек P₁ и Q₁ на прямую A₁B₁. Как известно,  ∠CB₁A₁ = ∠AB₁C₁;  значит,  ∠P₁B₁K = ∠P₁B₁C₁,  и прямоугольные треугольники P₁B₁K и P₁B₁C₁ равны по гипотенузе и острому углу. Отсюда  B₁K = B₁C₁.  Аналогично,  A₁L = A₁C₁,  то есть длина отрезка KL равна периметру 2p треугольника A₁B₁C₁.

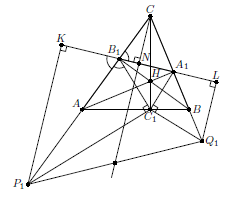
  Поскольку C – центр вневписанной окружности треугольника A₁B₁C₁, то N – точка касания этой окружности с A₁B₁, и  B₁N = p – B₁C₁  (см. задачу 155404). Значит,  KN = B₁C₁ + p – B₁C₁ = p.  Следовательно, N – середина отрезка KL, а прямая CN содержит среднюю линию прямоугольной трапеции KLQ₁P₁, что и требовалось.

Решение 2:   Обозначим  ∠BAC = α,  ∠ABC = β; тогда  ∠ACC₁ = 90° – α,  ∠BCC₁ = 90° – β.  Поскольку треугольники AB₁C₁, A₁BC₁ и ABC подобны, то

∠HPC = 90° – ∠AB₁C₁ = 90° – β  и, аналогично,  ∠HQC = 90° – α.  Наконец, пусть перпендикуляр из C на A₁B₁ пересекает PQ в точке X (рис. слева). Тогда  ∠PCX = 90° – β,  ∠QCX = 90° – α.

  Нам нужно доказать, что CX – медиана треугольника CPQ; поскольку  ∠PCX = ∠QCH,  это равносильно тому, что CH – симедиана. Итак, мы свели задачу к следующему факту.

  Лемма. Пусть в треугольнике CPQ точка H такова, что  ∠CPH = ∠QCH  и  ∠CQH = ∠PCH. Тогда CH – симедиана в этом треугольнике.

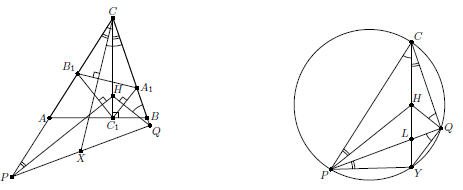
 Доказательство. Пусть L – точка пересечения CH и PQ (рис. справа). Тогда HL – биссектриса угла PHQ. Далее можно рассуждать по-разному.

  Первый способ. Треугольники PHC и CHQ подобны по двум углам. Следовательно, 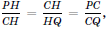 ,  откуда  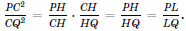  Таким образом, CH – симедиана (см. задачу 156978).

  Второй способ. Пусть описанная окружность треугольника CPQ пересекает CH вторично в точке Y (рис. справа). Тогда  ∠QPY = ∠QCY = ∠CPH,  аналогично,  ∠PQY = ∠CQH.  Следовательно, биссектрисы углов HPL и CPY совпадают, равно как и биссектрисы углов HQL и CQY. Поскольку HY – биссектриса угла PHQ, то биссектрисы углов CPY и CQY пересекаются на CY. Следовательно, 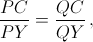    то есть четырёхугольник CPYQ – гармонический. Отсюда и следует требуемое утверждение (см. статью Я. Понарина "Гармонический четырёхугольник").

Ответ задачи отсутствует