1. Будем называть элементарным треугольник с площадью ½ и целыми квадратами сторон. Элементарный треугольник со сторонами 1, 1, и 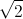   обозначим через Δ.

  Назовем переклейкой операцию разрезания треугольника ABC по медиане AM и склеивания получившихся треугольников ABM и ACM по равным отрезкам BM и CM в новый треугольник со сторонами AB, AC и 2AM.

  2. Покажем, что из любого элементарного треугольника δ можно переклейками получить Δ.

  Заметим, что переклейка переводит элементарный треугольник в элементарный: площадь не меняется, а из формулы  4m² = 2b² + 2c² – a²  следует, что целочисленность квадратов сторон тоже сохраняется.

  Будем переклеивать произвольный элементарный треугольник δ следующим образом: если у δ есть тупой угол, то будем разрезать его по медиане из этого угла. Тогда наибольшая сторона треугольника будет уменьшаться, и так как квадраты сторон целые, то когда-нибудь мы получим элементарный треугольник δ, являющийся прямоугольным или остроугольным. В этом случае синус наибольшего угла не меньше 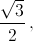   поэтому произведение сторон, прилегающих к нему, не больше  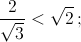   значит, они обе единичные, а тогда угол между ними – прямой. Таким образом, мы получили Δ.

  3. Если δ' получен переклейками из δ, то и δ можно получить переклейками из δ'. Следовательно, любой элементарный треугольник δ может быть получен переклейками из Δ.

  4. Будем называть треугольник δ оберткой, если квадрат со стороной ½ можно завернуть в δ так, чтобы каждые две точки, лежащие на одной стороне δ и равноудаленные от середины этой стороны, совместились.

  Треугольник Δ является оберткой: перегнём его по средним линиям, параллельным катетам.

  Предположим, что треугольник  δ = ABC  является оберткой, и пусть AM – одна из его медиан. Рассмотрим способ заворачивания в неё квадрата, склеим в нём все пары точек стороны BC, равноудалённые от M, и разрежем её вдоль AM. В результате получим, что переклейка треугольника ABC по медиане AM также является оберткой. Отсюда, вкупе с пунктом 3, следует утверждение задачи.

Ответ задачи отсутствует