Задача
Три велосипедиста ездят по кольцевой дороге радиуса 1 км против часовой стрелки с постоянными различными скоростями.
Верно ли, что, если они будут кататься достаточно долго, то найдётся момент, когда расстояние между каждыми двумя из них будет больше 1 км?
Решение
Если изменить скорости велосипедистов на одну и ту же величину, то расстояния между ними в любой момент времени останутся такими же. Поэтому можно считать, что первый велосипедист стоит на месте в некоторой точке A.
Впишем в данную окружность правильный шестиугольник ABCDEF и обозначим через M и N середины дуг BC и EF соответственно. Пусть второй и третий велосипедисты стартуют из точки M с равными скоростями в противоположных направлениях: второй – к точке B, третий – к точке C (см. рис. слева).
Пока они не достигли этих точек, расстояние между ними меньше 1 км. Затем второй велосипедист будет удален от первого, то есть от точки A, меньше, чем на 1 км, пока не приедет в точку F. Одновременно третий приедет в точку E, и расстояние между вторым и третьим станет равно 1 км. Затем оно уменьшается, пока велосипедисты не встретятся в точке N. Получили расположение, симметричное первоначальному относительно прямой AD, с переменой местами второго и третьего велосипедистов. Далее процесс повторяется.
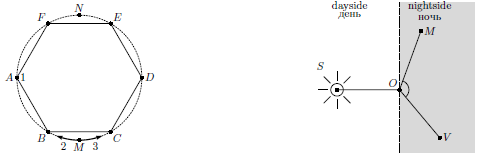
Ответ
Неверно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь